AI/ML Essentials Part1: Self-Organizing Maps#
This article is the start of a series that introduces different models and algorithms to beginners
Motivation#
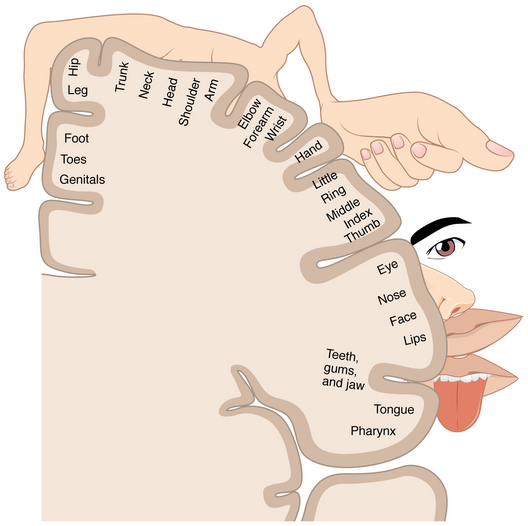
Figure 1: A graphical representation of the body mapped in the somatosensory cortex of the brain (source: OpenStax College).#
Artificial Intelligence and Machine Learning (AI/ML) often appear overly complex and sometimes may even be intimidating—including for those holding degrees in engineering or natural science. Formal descriptions of the underlying algorithms are math-heavy and rarely an easy read. Despite the need for scientific correctness, many concepts are in fact quite intuitive and feel organic (quite literally in this case). Once the beauty of the ideas becomes imminent, one can easily understand the fascination it holds for ML practitioners.
With this article, I want to excite your curiosity and incidentally introduce my favorite algorithm within this amazing scientific field: “self-organizing maps.”1 I promise to keep the amount of formalism and mathematics at a bare minimum.
Self-organizing maps (SOM) are used for unsupervised learning. This means that learning discovers structure in data on its own without teaching signals or labels. This is unlike forecasting and most deep learning techniques2, which all classify as supervised learning.
Like all artificial neural networks, SOM are inspired by neuroscience. They are drastically simplified simulations of layers of the very neurons we find in our brains. These artificial neurons mimic a specific behavior that can be observed by cortical neurons.
The Cerebral cortex (the brain’s surface) is arguably the most interesting part of our brain3. Neurons there naturally organize themselves into maps (in the sense of cartography) that represent physical entities such as the body or the environment.
Figure 1 shows a famous depiction of such a neural/cortical map of the body in the somatosensory cortex—the region mainly responsible for processing the sense of touch. In this specific part of the brain, points that lie close to each other on the surface of the body are wired to neurons that are also neighbors in the cortex and the same spot is represented only once, much like in a classical world map.
This article will explain the principles that lead to self-organization and present a small experiment that I conducted recently when implementing the algorithm in Rust as an exercise.4
Concepts#
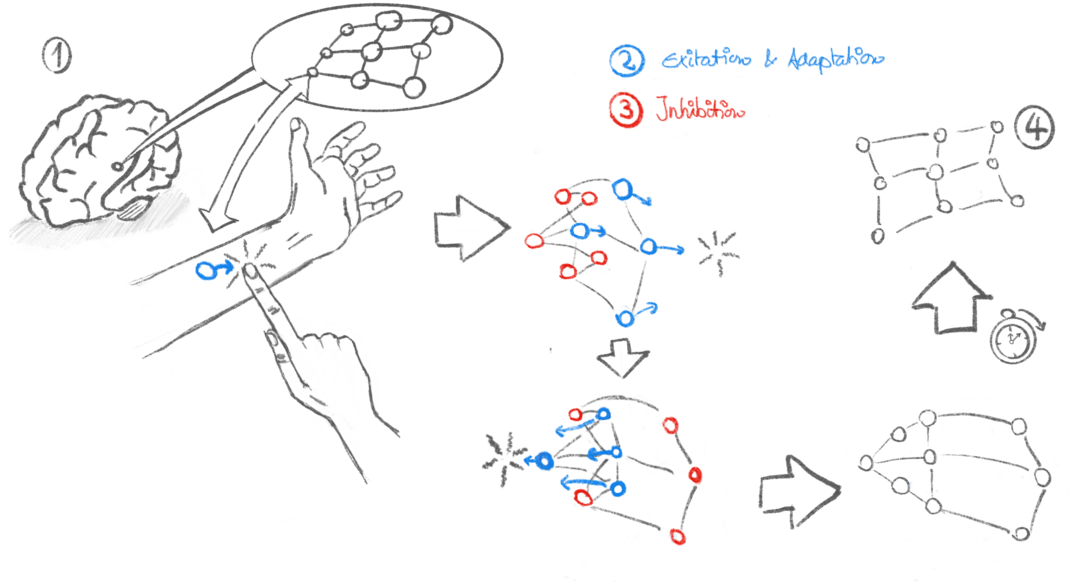
Figure 2: Illustration of excitation and lateral inhibition, the mechanisms that lead to self-organization.#
The concepts behind SOM can be explained in biological terms, and I think it’s an entertaining and intuitive approach that even avoids most technical terms and formulas. Keep in mind though that SOM are all but a model of a biological process. Consequently, the following should be considered a crude simplification—at the very best. We will choose the processing of touch on the left forearm as an example. Figure 2 shows an illustration of the complete concept and mechanisms.
Neurons are responsive ①. They are wired to sensors that capture input from the outside world and react to incoming signals with varying levels of intensity. They are tuned to specific sensor patterns, which stimulate them most, and gradually adapt to new patterns by altering synapses (biologists call this neural plasticity). In our example, this means that each neuron corresponds to a small area of your forearm and responds when it is touched. On adaptation, this receptive field wanders toward the new input in a neural map; neurons can influence their near neighbors so that they all tune to similar inputs ②. We say that a neuron excites its neighbors. The intensity, however, decreases with the physical distance between the neurons. That excitation alone already ensures that neighbors will eventually react to similar stimuli—an important requirement of maps in general.
It does not, however, guarantee exclusiveness: Distant neurons might be identically tuned, and this ambiguity needs to be avoided. The mechanism that prevents this from happening is referred to as lateral inhibition by neurobiologists ③.
Each time the network is exposed to an input signal, there will be a single neuron that happens to be tuned best to it. It is sometimes called the winning neuron or best matching unit (BMU). It is also the first to react and can inhibit adaptation in all other neurons except for its near neighbors.
Thanks to those two simple mechanisms, the map will slowly “unfold” during an exploration phase ④: Neurons correspond to areas that are evenly distributed on the skin and reflect how the neurons are organized.
We can create functional models of neural maps by translating these properties into mathematical expressions and implementing them in software. As you surely will have guessed SOM are a model for neural maps, and one algorithm (mentioned below) to train them implements the principles described above. In brief, it follows a few simple steps and can be written in little more than 10 lines of Python code.5
Represent the model as two list of vectors of equal length. One holds the physical positions of the neurons, which are the coordinates of the vertices of a regular grid; the other holds the tuning patterns and is initialized with random values from the input space (this list is often called the “codebook”).
Pick a random input sample from the training data. Determine the BMU by comparing with the vectors in the codebook. On the technical side, SOM are not limited to two-dimensional topologies of neurons, although rarely more than three are feasible (there are variations that overcome this limitation). The codebook vectors, in contrast, can be very high dimensional. SOM have a broad range of application. They are still commonly used for visualization and dimensionality reduction, clustering, and more exotic tasks in robotics or machine vision.
Adapt the BMU and its nearest neighbors by shifting their codebook vectors toward the input. The movement must be weighted in relation to the distance between the neuron and the BMU. Typically, this involves a Gaussian bell function.
Repeat steps 2 and 3 but each time weaken the effect of adaptation and decrease the influence of the BMU on its neighbors over time. Terminate on convergence.
Self-organization seems to be a common principle in the brain. Another prominent example is the place cells, which enable mammals to map and navigate through mazes, and whose discovery has been awarded with a Nobel price not long ago.6 In the next section, I will show that something slightly similar can be achieved with SOM.
On the technical side, SOM are not limited to two-dimensional topologies of neurons, although rarely more than three are feasible (there are variations that overcome this limitation). The codebook vectors, in contrast, can be very high dimensional.
SOM have a broad range of application. They are still commonly used for visualization and dimensionality reduction, clustering, and more exotic tasks in robotics or machine vision.
Showcase: A Model for Place Cells#
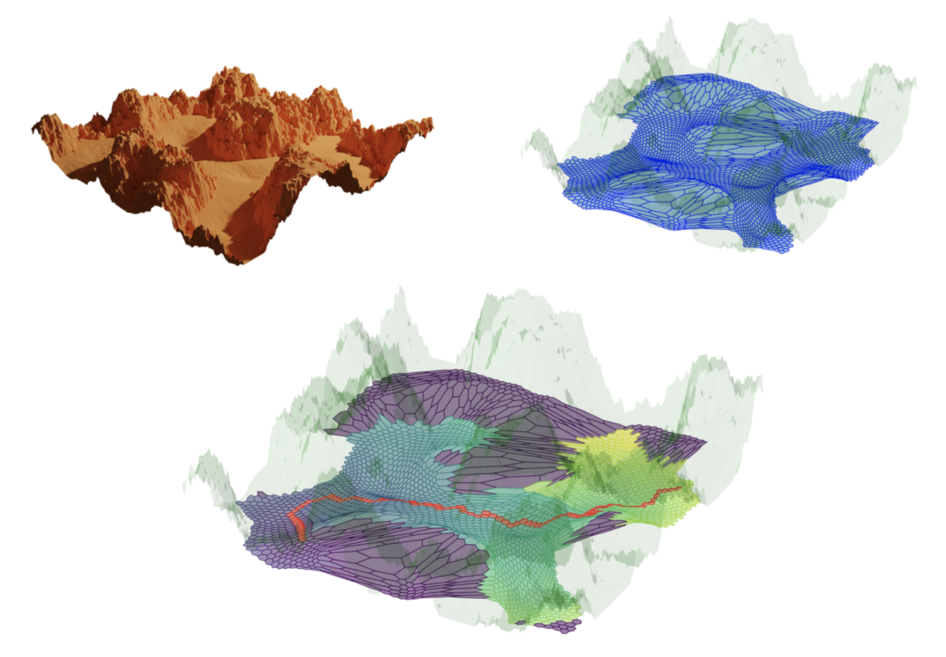
Figure 3: Artificial place cell experiment. Upper left: A randomly generated labyrinth in a canyon landscape. Upper right: A (hexagonal) self-organizing map that mimics mammalian place cells and learned all accessible areas. Bottom: The shortest path between two remote locations in the map.#
Let me show you how simple principles like those behind the SOM can often solve surprisingly complex tasks. To do that, we mimic the place cells that I mentioned above. The experiment includes a labyrinth in a canyon landscape that I quickly generated in a 3D modeling software.7 The problem to be solved is how to find the shortest path to get from one remote area to another. The whole experiment is shown in Figure 3.
At first, one needs to acquire random sample points from the map but only from areas that are accessible. For the sake of simplicity, I just filtered by height to detect the ground. A SOM is trained on these samples. I made a slight modification to the original algorithm: The neurons are physically arranged in a hexagonal pattern. This is closer to the biological prototype and looks more organic and “way cooler”. As can be seen in the top right, learning a map is not a challenge at all. All neurons distribute evenly on the accessible surface, and we can now exploit the neighborhood relations for the task of finding the shortest route between two points.
Therefore, we need to operate on the learned map. We could use algorithms such as the famous Dijkstra algorithm, which is used in navigation systems, or we could opt for something simpler and more natural. Let me outline the idea, which I think is beautiful because of its simplicity: Imagine that the neurons behaved like elementary school kids on a school yard. The neuron representing the target position suddenly starts pushing all its immediate neighbors (again, by excitation). The neighbors now start exciting their own neighbors in response. The chaos that emerges propagates like a wave through the network, until the neuron representing the start position notices the other neurons’ behaviors around it. By successively asking who started first, the shortest path can be traced back to the original perpetuator.
The only thing that needs to be taken care of first is to disconnect the neighboring neurons that are separated by mountain: I used a threshold on the size of the hexagons.
This method is called the Wavefront algorithm, and in my opinion, it harmonizes extremely well with the SOM approach. Moreover, it is highly parallel by nature and is very easy to implement.8 In Figure 3, the wave is depicted as it traveled through the network. Lighter colors indicate later activation.
Written in a very few lines of code, this implementation can be used as an AI component that controls characters in a video game that don’t get stuck behind obstacles and optimally reach their targets. But it could be applied in a more serious application such as a search and rescue mission in difficult terrain after a natural disaster. Naturally, it is not that easily applied to the real world, but I hope this example still demonstrates how ML-based approaches can solve some complex problems in a very elegant way.
Conclusion#
In my opinion, most AI/ML methods usually are not as intimidating as they might appear at first. Many of them are built on simple and intuitive principles, and the complexity chimes in only for mathematical proofs and optimization.
Deep learning, for instance, comes in an overwhelming quantity of (sometimes short-lived) complex variations. However, at the end of the day, these variants are all based on the same artificial neurons that are not too different from those we have seen in this article (consider them as their cousins that are good at supervised learning). For me, the principle of self-organization holds a certain fascination despite (or may be precisely because of) its simplicity, and I still use it quite regularly in robotic projects.
With this article, I hope I managed to attract your curiosity for the amazing field of AI/ML and the creative methods within. Please feel encouraged to try and implement a few of them. This is an excellent exercise and the best way to get a solid understanding and “feeling” of how to use AI/ML effectively.
- 1
Also known as Kohonen maps named after their inventor Teuvo Kohonen (†13.12.2021). His book about SOM is freely available
- 2
In general, all methods for regression (predicting numbers) and classification (predicting things).
- 3
Evolution even gave it wrinkles so that we can have more of it crammed into the skull.
- 4
The project is intended to serve as a stencil for numerical Python extensions written in Rust.
- 5
I recommend trying this for yourself as a short, fun, and quite rewarding exercise.
- 6
John O’Keefe, and May-Britt and Edvard I. Moser in 2014.
- 7
www.blender.org
- 8
Again, a very good exercise.